Minggu, 04 November 2012

Kombinasi,Permutasi,Teorema Bayes dam Macam2 Bilangan

Kombinasi adalah menggabungkan beberapa objek dari suatu grup tanpa memperhatikan urutan. Di dalam kombinasi, urutan tidak diperhatikan.
{1,2,3} adalah sama dengan {2,3,1} dan {3,1,2}.
Contoh: Seorang anak hanya diperbolehkan mengambil dua buah amplop dari tiga buah amplop yang disediakan yaitu amplop A, amplop B dan amplop C. Tentukan ada berapa banyak kombinasi untuk mengambil dua buah amplop dari tiga buah amplop yang disediakan?
Solusi: Ada 3 kombinasi yaitu; A-B, A-C dan B-C.
Sedangkan permutasi adalah menggabungkan beberapa objek dari suatu grup dengan memperhatikan urutan. Di dalam permutasi, urutan diperhatikan.
{1,2,3} tidak sama dengan {2,3,1} dan {3,1,2}
Contoh: Ada sebuah kotak berisi 3 bola masing-masing berwarna merah, hijau dan biru. Jika seorang anak ditugaskan untuk mengambil 2 bola secara acak dan urutan pengambilan diperhatikan, ada berapa permutasi yang terjadi?
Solusi: Ada 6 permutasi yaitu; M-H, M-B, H-M, H-B, B-M, B-H.
Salah satu aplikasi kombinasi dan permutasi adalah digunakan untuk mencari probabilitas suatu kejadian.

Permutasi pengulangan

Jika urutan diperhatikan dan suatu objek dapat dipilih lebih dari sekali maka jumlah permutasinya adalah:
n^r \,
di mana n adalah banyaknya objek yang dapat dipilih dan r adalah jumlah yang harus dipilih.
Sebagai contoh, jika kamu memiliki huruf A, B, C, dan D dan kamu ingin mencari tahu ada berapa cara untuk menyusunnya dalam suatu grup yang berisi tiga angka maka kamu akan menemukan bahwa ada 43 atau 64 cara untuk menyusunnya. Beberapa cara untuk menyusunnya adalah: AAA, BBB, CCC, DDD, ABB, CBB, DBB, dst.

Permutasi tanpa pengulangan

Jika urutan diperhatikan dan setiap objek yang tersedia hanya bisa dipilih atau dipakai sekali maka jumlah permutasi yang ada adalah:
\frac{n!}{(n-r)!}
di mana n adalah jumlah objek yang dapat kamu pilih, r adalah jumlah yang harus dipilih dan ! adalah simbol faktorial.
Sebagai contoh, ada sebuah pemungutan suara dalam suatu organisasi. Kandidat yang bisa dipilih ada lima orang. Yang mendapat suara terbanyak akan diangkat menjadi ketua organisasi tersebut. Yang mendapat suara kedua terbanyak akan diangkat menjadi wakil ketua. Dan yang mendapat suara ketiga terbanyak akan menjadi sekretaris. Ada berapa banyak hasil pemungutan suara yang mungkin terjadi? Dengan menggunakan rumus di atas maka ada 5!/(5-3)! = 60 permutasi.
Umpamakan jika n = r (yang menandakan bahwa jumlah objek yang bisa dipilih sama dengan jumlah yang harus dipilih) maka rumusnya menjadi:
\frac{n!}{(n-n)!} = \frac{n!}{0!} = n! karena 0! = 1! = 1
Sebagai contoh, ada lima kotak kosong yang tersedia. Kelima kotak kosong itu harus diisi (tidak boleh ada yang kosong). Kelima kotak kosong itu hanya boleh diisi dengan angka 1,2,3,4,5. Ada berapa banyak cara untuk mengisi kotak kosong? Dengan menggunakan rumus n! maka ada 5! = 120 permutasi.

Kombinasi tanpa pengulangan

Ketika urutan tidak diperhatikan akan tetapi setiap objek yang ada hanya bisa dipilih sekali maka jumlah kombinasi yang ada adalah:
{{n!} \over {r!(n - r)!}} = {n \choose r}
Di mana n adalah jumlah objek yang bisa dipilih dan r adalah jumlah yang harus dipilih.
Sebagai contoh, kamu mempunyai 5 pensil warna dengan warna yang berbeda yaitu; merah, kuning, hijau, biru dan ungu. Kamu ingin membawanya ke sekolah. Tapi kamu hanya boleh membawa dua pensil warna. Ada berapa banyak cara untuk mengkombinasikan pensil warna yang ada? Dengan menggunakan rumus di atas maka ada 5!/(5-2)!(2)! = 10 kombinasi.

Kombinasi pengulangan

Jika urutan tidak diperhatikan dan objek bisa dipilih lebih dari sekali, maka jumlah kombinasi yang ada adalah:
{{(n + r - 1)!} \over {r!(n - 1)!}} = {{n + r - 1} \choose {r}} = {{n + r - 1} \choose {n - 1}}
Di mana n adalah jumlah objek yang bisa dipilih dan r adalah jumlah yang harus dipilih. Sebagai contoh jika kamu pergi ke sebuah toko donat. Toko donut itu menyediakan 10 jenis donat berbeda. Kamu ingin membeli tiga donat. Maka kombinasi yang dihasilkan adalah (10+3-1)!/3!(10-1)! = 220 kombinasi.

Kombinasi C dari sebuah himpunan S adalah himpunan bagian dari S.
C \subseteq S
Sebagai contoh, misalkan terdapat suatu kumpulan buah: apel, jeruk, mangga, pisang. Maka {apel, jeruk} dan {jeruk, mangga, pisang} adalah merupakan kombinasi dari kumpulan tersebut. Seluruh himpunan bagian yang mungkin dibentuk dari kumpulan buah tersebut adalah:
  • tidak ada buah apa pun
  • satu buah:
    • apel
    • jeruk
    • mangga
    • pisang
  • dua buah:
    • apel, jeruk
    • apel, mangga
    • apel, pisang
    • jeruk, mangga
    • jeruk, pisang
    • mangga, pisang
  • tiga buah:
    • apel, jeruk, mangga
    • apel, jeruk, pisang
    • apel, mangga, pisang
    • jeruk, mangga, pisang
  • empat buah:
    • apel, jeruk, mangga, pisang
Kombinasi r dari sebuah himpunan S, berarti dari himpunan S diambil elemen sebanyak r untuk dijadikan sebuah himpunan baru. Dalam hal kumpulan buah di atas, himpunan {apel, jeruk, pisang} adalah sebuah kombinasi 3 dari S, sedangkan {jeruk, pisang} adalah sebuah kombinasi 2 dari S.
Banyaknya kombinasi r dari sebuah himpunan berisi n elemen dapat dihitung tanpa harus memperhatikan isi dari himpunan tersebut. Besarnya dinyatakan dengan fungsi:
C_r^n = \frac{n!}{r!(n-r)!}
Fungsi C_r^n dalam banyak literatur dinyatakan juga dengan notasi {n \choose r}.
Sebagai contoh, tanpa harus mengetahui elemen himpunan {apel, jeruk, mangga, pisang}, banyaknya kombinasi 3 dari himpunan tersebut dapat dihitung:
C_3^4 = \frac{4!}{3!(4-3)!} = 4

Sifat rekursif dari Kombinasi

Kombinasi dapat dibentuk dari dua kombinasi sebelumnya. Ini mengakibatkan banyaknya kombinasi juga bersifat rekursif:
C^n_r = C^{n-1}_{r-1} + C^{n-1}_{r}

Hubungan dengan Permutasi

Dari himpunan {apel, jeruk, mangga, pisang} dapat diambil permutasi 3 unsur, yang dapat didaftar sebagai berikut:
apel jeruk mangga apel mangga jeruk jeruk apel mangga jeruk mangga apel mangga apel jeruk mangga jeruk apel
apel jeruk pisang apel pisang jeruk jeruk apel pisang jeruk pisang apel pisang apel jeruk pisang jeruk apel
apel mangga pisang apel pisang mangga mangga apel pisang mangga pisang apel pisang apel mangga pisang mangga apel
jeruk mangga pisang jeruk pisang mangga mangga jeruk pisang mangga pisang jeruk pisang jeruk mangga pisang mangga jeruk
Perhatikan bahwa dalam susunan ini setiap kolom merupakan permutasi dari kolom pertama. Karena dalam kombinasi urutan tidak dipentingkan, maka cukup salah satu kolom saja yang diambil. Jika kita mengambil kolom pertama saja, maka kita mendapatkan kombinasi 3 dari keempat buah tersebut adalah:
  • apel, jeruk, mangga
  • apel, jeruk, pisang
  • apel, mangga, pisang
  • jeruk, mangga, pisang
Penyusunan tabel seperti di atas akan menghasilkan P ^4_3 atau 24 permutasi, dengan 3 ! kolom, karena untuk setiap baris terdapat 3 ! permutasi dari kolom pertama. Dengan demikian, jumlah baris dari tabel akan sebesar:
\frac{P ^4_3}{3!}
Aturan seperti ini dapat digeneralisasikan sehingga untuk setiap n unsur yang dikombinasikan r unsur, berlaku:
C^n_r = \frac{P^n_r}{r!}
Yang dapat dengan mudah dibuktikan:
C^n_r = \frac{P^n_r}{r!}
= \frac{\frac{n!}{(n-r)!}}{r!}
= \frac{n!}{r! (n-r)!}

Hubungan dengan Permutasi Berunsur Identik

Kombinasi juga berhubungan dengan permutasi dengan unsur identik. Kombinasi dari sebuah himpunan S dapat dimengerti sebagai pemilihan unsur-unsur himpunan S. Unsur yang terpilih kita tandai dengan 1, dan yang tidak terpilih kita tandai dengan 0. Dengan demikian dari himpunan {apel, jeruk, mangga, pisang} tersebut, kita dapat mendaftarkan kombinasi-3 nya seperti ini:
Kombinasi apel jeruk mangga pisang
apel, jeruk, mangga 1 1 1 0
apel, jeruk, pisang 1 1 0 1
apel, mangga, pisang 1 0 1 1
jeruk, mangga, pisang 0 1 1 1
Dengan demikian, banyaknya kombinasi 3 unsur dari himpunan S yang berisi 4 benda setara dengan banyaknya permutasi terhadap untai 1110, yaitu:
\frac{4!}{3!} = 4
Karena untai 1110 memiliki 4 unsur, tetapi ada 3 unsur identik, yaitu 1. Maka total permutasinya adalah 4! dibagi dengan 3!. Kombinasi r dari n unsur, sesuai dengan pengertian itu, selalu setara dengan permutasi yang terdiri dari r angka 1 dan n - r angka 0. Maka permutasinya menjadi:
\frac{n!}{r! (n-r)!}
Yang sesuai dengan rumus kita di awal, untuk menghitung C^n_r.

Koefisien Binomial

Suatu binomial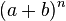 (a + b)^n yang dijabarkan dalam bentuk jumlahan, akan membangkitkan koefisien-koefisien yang merupakan bilangan kombinasi.
(a + b)^n = \sum_{k = 0}^{n} {n \choose k} a^{n-k} b^k
Dengan penjabaran seperti di atas, maka banyaknya kombinasi r dari n unsur bisa didapat dari setiap suku:
{n \choose r} = \mbox{koefisien } a^{r} b^{n-r}
Daftar berikut menunjukkan beberapa penjabaran binomial:
  1. (a + b)^0 = 1a^0b^0
  2. (a + b)^1 = 1a^1b^0 + 1a^0b^1
  3. (a + b)^2 = 1a^2b^0 + 2a^1b^1 + 1a^0b^2
  4. (a + b)^3 = 1a^3b^0 + 3a^2b^1 + 3a^1b^2 + 1a^0b^3
  5. (a + b)^4 = 1a^4b^0 + 4a^3b^1 + 6a^2b^2 + 4a^1b^3 + 1a^0b^4
  6. (a + b)^5 = 1a^5b^0 + 5a^4b^1 + 10a^3b^2 + 10a^2b^3 + 5a^1b^4 + 1a^0b^5
  7. (a + b)^6 = 1a^6b^0 + 6a^5b^1 + 15a^4b^2 + 20a^3b^3 + 15a^2b^4 + 6a^1b^5 + 1a^0b^6

Segitiga Pascal

Dengan menuliskan hanya koefisiennya saja, dari penjabaran binomial dapat kita peroleh:
  1. (a + b)^0 = 1a^0b^0 \rightarrow 1
  2. (a + b)^1 = 1a^1b^0 + 1a^0b^1 \rightarrow 1, 1
  3. (a + b)^2 = 1a^2b^0 + 2a^1b^1 + 1a^0b^2 \rightarrow 1, 2, 1
  4. (a + b)^3 = 1a^3b^0 + 3a^2b^1 + 3a^1b^2 + 1a^0b^3 \rightarrow 1, 3, 3, 1
Jika diteruskan, daftar koefisien ini akan membentuk susunan yang disebut sebagai Segitiga Pascal.
         1
        1  1
       1  2  1
      1  3  3  1
     1  4  6  4  1
    1  5 10 10  5  1
   1  6 15 20 15  6  1
  1  7 21 35 35 21  7  1
 1  8 28 56 70 56 28  8  1


Teorema Bayes

Teorema Bayes, diambil dari nama Rev. Thomas Bayes, menggambarkan hubungan antara peluang bersyarat dari dua kejadian A dan B sebagai berikut:
P(A | B) = P(B | A) P(A)
P(B)
or
P(A | B) = P(B | A) P(A)
P(B | A)P(A) + P(B | A)P(A)
Contoh aplikasi dari Teorema Bayes
Di sebuah negara, diketahui bahwa 2% dari penduduknya menderita sebuah penyakit langka. 97% dari hasil tes klinik adalah positif bahwa seseorang menderita penyakit itu. Ketika seseorang yang tidak menderita penyakit itu dites dengan tes yang sama, 9% dari hasil tes memberikan hasil positif yang salah.
Jika sembarang orang dari negara itu mengambil test dan mendapat hasil positif, berapakah peluang bahwa dia benar-benar menderita penyakit langka itu?
Secara sepintas, nampaknya bahwa ada peluang yang besar bahwa orang itu memang benar-benar menderita penyakit langka itu. Karena kita tahu bahwa hasil test klinik yang cukup akurat (97%). Tetapi apakah benar demikian? Marilah kita lihat perhitungan matematikanya.
Marilah kita lambangkan informasi di atas sebagai berikut:
  • B = Kejadian tes memberikan hasil positif.
  • B = Kejadian tes memberikan hasil negatif.
  • A = Kejadian seseorang menderita penyakit langka itu.
  • A = Kejadian seseorang tidak menderita penyakit langkat itu.
Kita ketahui juga peluang dari kejadian-kejadian berikut:
  • P (A) = 2%
  • P (A) = 98%
  • P (B | A) = 97%
  • P (B | A) = 9%
Dengan menggunakan rumus untuk peluang bersyarat, dapat kita simpulkan peluang dari kejadian-kejadian yang mungkin terjadi dalam tabel di bawah ini:

A (2%)A (98%)
BPositif yang benar
P (B ∩ A) = P (A) × P (B | A) = 2% × 97% = 0,0194		 Positif yang salah
P (B ∩ A) = P (A) × P (B | A) = 98% × 9% = 0,0882
BNegatif yang salah
P (B ∩ A) = P (A) × P (B | A) = 2% × 3% = 0,0006		Negatif yang benar
P (B ∩ A) = P (A) × P (B | A) = 98% × 91% = 0,8918
Misalnya seseorang menjalani tes klinik tersebut dan mendapatkan hasil positif, berapakah peluang bahwa ia benar-benar menderita penyakit langka tersebut?
Dengan kata lain, kita mencoba untuk mencari peluang dari A, dimana B atau P (A | B).
Dari tabel di atas, dapat kita lihat bahwa P (A | B) adalah peluang dari positif yang benar dibagi dengan peluang positif (benar maupun salah), yaitu 0,0194 / (0,0194 + 0,0882) = 0,1803.
Kita dapat juga mendapatkan hasil yang sama dengan menggunakan rumus teorema Bayes di atas:
P(A | B) = P(B ∩ A)
P(B)
= P(B | A) × P(A)
P(B | A)P(A) + P(B | A)P(A)
= 97% × 2%
(97% × 2%) + (9% × 98%)
= 0.0194
0.0194 + 0.0882
= 0.0194
0.1076
P(A | B) = 0.1803
Hasil perhitungan ini sangat berbeda dengan intuisi kita di atas. Peluang bahwa orang yang mendapat hasil tes positif itu benar-benar menderita penyakit langka tidak sebesar yang kita bayangkan. Cuma ada sekitar 18% kemungkinan bahwa dia benar-benar menderita penyakit itu.
Mengapakah demikian?
Ketika mengira-ngira peluangnya, seringkali kita lupa bahwa dari seluruh populasi negara itu, hanya 2% yang benar-benar menderita penyakit langka itu. Jadi, walaupun hasil tes adalah positif, peluang bahwa seseorang menderita penyakit langka itu tidaklah sebesar yang kita bayangkan.
Kita bisa juga meninjau situasi di atas sebagai berikut. Misalnya populasi negara tersebut adalah 1000 orang. Hanya 20 orang yang menderita penyakit langka itu (2%). 19 orang dari antaranya akan mendapat hasil tes yang positif (97% hasil positif yang benar). Dari 980 orang yang tidak menderita penyakit itu, sekitar 88 orang juga akan mendapat hasil tes positif (9% hasil positif yang salah).
Jadi, 1000 orang di negara itu dapat kita kelompokkan sebagai berikut:
  • 19 orang mendapat hasil tes positif yang benar
  • 1 orang mendapat hasil tes negatif yang salah
  • 88 orang mendapat hasil tes positif yang salah
  • 892 orang mendapat hasil tes negatif yang benar
Bisa kita lihat dari informasi di atas, bahwa ada (88 + 19) = 107 orang yang akan mendapatkan hasil tes positif (tidak perduli bahwa dia benar-benar menderita penyakit langka itu atau tidak). Dari 107 orang ini, berapakah yang benar-benar menderita penyakit? Hanya 19 orang dari 107, atau sekitar 18%.
 
BILANGAN
Dalam bidang Matematika, bilangan dapat diklasifikasikan atau digolongkan ke dalam beberapa jenis atau kelompok: bilangan kompleks numbers, bilangan imajiner, bilangan riil, bilangan rasional, bilangan irasional, bilangan bulat, bilangan asli, dan bilangan cacah.
Bilangan Asli dan Bilangan Cacah (ℕ)
Ada dua definisi bilangan asli:
  • elemen dari himpunan { 1, 2, 3, 4, ... }
  • elemen dari himpunan { 0, 1, 2, 3, 4, ... }
Definisi yang pertama tidak memasukkan 0 (nol), sedangkan definisi yang kedua memasukkan 0 (nol). Definisi yang kedua (yang memasukkan 0) dapat juga disebut bilangan cacah. Sayangnya, tidak ada kesepakatan yang disetujui oleh semua ahli matematika sampai sekarang. Untuk lebih jelas gunakanlah istilah bilangan bulat positif (tidak termasuk 0) dan bilangan bulat yang tidak negatif (termasuk 0).
Contoh: 1, 2, 4, 7, dst.
Bilangan bulat (ℤ)
Bilangan yang dapat ditulis tanpa menggunakan pecahan atau dalam bentuk desimal. Bilangan bulat terdiri atas bilangan asli, negatifnya, dan bilangan nol.
ℤ = { ..., -2, -1, 0, 1, 2, ... }.
Bilangan bulat dilambangkan dengan simbol ℤ yang berasal dari bahasa Jerman: Zahlen (yang berarti "bilangan").
Contoh: -12, -3, 0, 4, 5, dst.
Bilangan Rasional (ℚ)
Bilangan yang dapat dinyatakan sebagai pecahan. Dilambangkan dengan simbol ℚ dari kata bahasa Inggris quotient yang berarti "hasil bagi".
Contoh: -23, -3,5, 0, 2, 2¾, 4.7, dst.
Bilangan Irasional
Bilangan yang tidak dapat dinyatakan sebagai pecahan.
Contoh: √2, √3, π, e, dst.
Bilangan Riil (ℝ)
Bilangan yang memiliki korespondensi satu-satu dengan titik-titik yang terletak pada garis bilangan tak terbatas. Himpunan bilangan riil terdiri atas bilangan rasional dan bilangan irasional. Dengan kata lain, bilangan riil adalah bilangan yang dapat dituliskan dalam bentuk desimal.
Contoh: √2, -3,4, 1, dst.
Bilangan Imajiner
Bilangan yang kuadratnya adalah bilangan riil negatif. Bilangan imajiner dituliskan dengan simbol i, dimana i = √-1.
Contoh : 2i, -4i, 5i, dst.
Bilangan Kompleks (ℂ)
Bilangan yang berbentuk a + bi, dimana a dan b adalah bilangan riil dan i adalah unit imajiner (i = √-1).
Contoh: 2 + 3i.



Diposting oleh di

2 komentar:

  1. JS1 September 2015 pukul 21.34

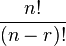
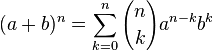
    Sebagian dari artikel ini (tentang Teorema Bayes dan tentang bilangan) telah diplagiat dari artikel asli I Do Maths Indonesia yang ada di http://www.idomaths.com/id/peluang5.php dan di http://www.idomaths.com/id/bilangan.php. Penulis harap segera menghapus bagian yang merupakan jiplakan atau pemilik I Do Maths akan mengambil tindakan lanjut.

    BalasHapus
  2. yemonhaberl3 Maret 2022 pukul 16.05

    The Casino - Jtm Hub
    The Casino is in the city centre and 충청북도 출장샵 it has 평택 출장마사지 lots of shops. 전라북도 출장마사지 It has some nice shops and great 안산 출장샵 services. We also have 춘천 출장마사지 a wide variety of special offers to

    BalasHapus

Langganan: Posting Komentar (Atom)